1. 배관 열응력 Quick Check 방법/공식 소개
공식 LFlex = 0.0254 * (T*L*S)1/2는 본인이 오랜 경험을 통하여,
배관 설계에서 배관의 열팽창 응력을 간단히 Check할 수 있도록 만든 공식입니다. 이 공식을 앞으로 Flex L
공식으로 부를 것입니다. 여기에서
| |
T: 배관의 온도(C), L: 열팽창과 관련한 배관의 길이(m),
S: 배관의 사이즈(인치)
LFlex:
배관이 길이 L에 의하여 팽창될 때 이 팽창량이 흡수될 수 있는 최소 길이(m)
|
|
|
위 공식에서 LFlex가 확보되지 않으면 그 배관은 굽힘을 많이 받게 됨으로 Stress를
많이 받게됩니다. 이 공식에 대한 재료 역학적 이론은 아래 "3. 위에서 사용한 Flex L 공식에 대한 재료역학적
근거"에서, 자세하게 설명하였으니 참고하시기 바랍니다. 다음은 이 공식을 활용하여 배관의 열응력을
빠르게 Check해 보는 문제들입니다.
|
문제 1.1
다음 그림의 배관 Route에서 거리 5000인 점에 가이드를 두고 싶다. Guide Support가 가능한가를 판정하라.
|
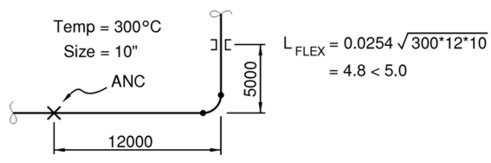
풀이 1.1
위 그림에서 12m의 열팽창으로 Guide 부위의 배관은 열응력을 받는다. 위 그림에 보인 바와 같이 Flex L 공식으로 계산하면
LFlex은4.8m 이다. 이 값은 12m의 열팽창에 대하여 Elbow에서 Guide까지의 거리가 4.8m 이상이면 Guide 부위에서 배관이 받는
Stress 값이 적어도 Allowable Stress 값 이상으로 되지는 않음을 의미한다. 따라서 Elbow로부터 5m 떨어진 지점에 가이드를
두어도 좋다.
|
문제 1.2
다음과 같은 배관 Route에서 거리 3000되는 곳에 Support를 해야 한다. Spring Support가 아닌 Rigid Support가
가능한가를 판정하라.
|
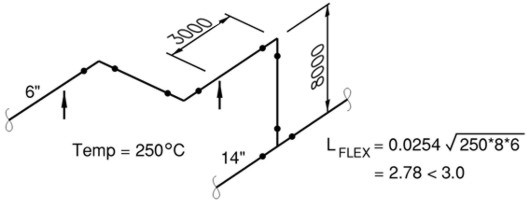
풀이 1.2
6"에 대하여 사이즈가 큰 14"는 ANC로 작용함으로, 열팽창의 길이를 8m로 보고 Flex L 공식으로 유연성 길이를
계산하면 위 그림에 보인 바와 같이 Flexible Length는 2.78m로 계산된다. 따라서 3.0m 지점에 Rigid Support를 해도 좋다.
그러나 Stress Analysis 결과 이 Support 지점에서 배관이 위로 들릴 경우, Spring Support를 해 주는 것이 바람직하다.
위로 들리는 +Y-Stop Support를 할 경우에는, 이 지점에 Support가 없는 경우로 Computer 응력해석을 해본 결과,
자중/압력에 대한 응력이 허용응력 이하이면 +Y-Stop을 둘 수 있다. 만약 자중/압력에 대한 응력이 허용응력 이상인 경우
Spring Support를 쓰거나 위아래를 모두 구속하는 Y-Stop을 두어야 한다. 즉, Flex L 공식에 의한 유연성이 요구되는
Min. Length는 이 지점을 구속해도 열응력이 적어도 허용응력 이상으로 되지 않음으로 위아래를 모두 잡는
Hold-Down Support가 가능함을 의미한다.
|
문제 1.3
다음과 같은 배관 Loop가 있다. 이 루프의 크기가 적절한가를 판정하라.
|
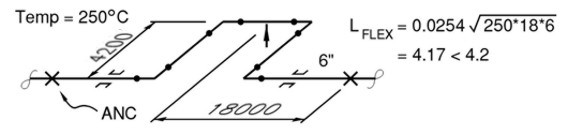
풀이 1.3
루프의 (Rigid Support가 있는) 중간 지점에서는 열팽창으로 인한 이동량이 없다. 따라서 배관 1.8m 구간에서
배관의 열 팽창량은 4.2m 구간에서 흡수되어야 한다. Flex L 공식으로 이를 체크하면 위 그림에 보인 바와 같이
유연성이 요구되는 길이는 4.17m로 계산된다. 따라서 이 Loop는 적절하다.
|
2. 배관응력과 관련한 재료역학의 주요공식
Stress
배관, 철골 구조물 등에 외력이 가해지면 구조물에는 가해지는 외력에 따라 외부 힘의 작용에 저항하는 (응답하는)
내력(수직력/전단력)이 발생하는데, 이를 응력(Stress)이라 하고, 압력단위와 같은, 단위 면적당 받는 힘으로 표현한다.
압력에는 음(-)압이 있으나 응력에는 음(-)의 응력은 없다. 이 응력은 구조물이 굽힘을 받을 때 크게 주어진다.
|
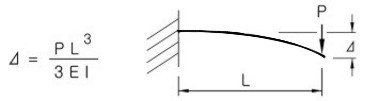
1. 외팔보의 처짐 공식
| |
 |
|
P: 외팔보의 끝단에 가해지는 힘
L: 외팔보의 길이
E: 재질의 탄성계수
I:
단면 2차 모멘트(Moment of Inertia),
I = ∫R2dA
|
2. Bending Stress Sb = M / Z
| |
M: 굽힘 작용을 하는 Moment
Z: 단면계수; Z = I / R
R: 도심에서 최 외곽 지점까지의 거리, 대칭인 경우 반경
|
3. Torsional Stress
St = T / ( IP / R)
|
|
T:
토크 (Torque; 모멘트에 의하여 발생한 회전력)
IP: Polar Moment of Inertia
|
4. 단면 2차 모멘트(Moment of Inertia,
I =
∫ R2dA)의 특성:
| |
|
| |
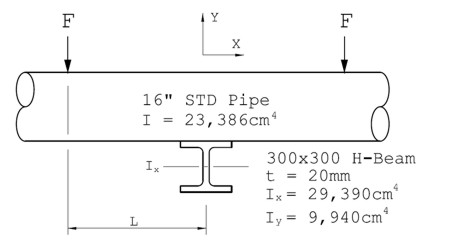
위의 그림에서 배관과 H-Beam의 재질이 같다고 가정하자. 중심으로부터 거리 L인 곳에 힘 F가 가해지면
이 배관은 굽힘 모멘트 M = L x F를 받는다. 아래 H-Beam에도 같은 거리(L)의 곳에 H-Beam의 지지점이
위치하면 배관과 H-Beam은 같은 굽힘 모멘트를 받는다. 힘 F를 점점 더 증가시키면 결국 둘 중에 어느
하나는 부러질 것이다. 배관과 Beam 중 어느 것이 굽힘에 더 강할까? 해답은 단면 2차 모멘트의 값이
큰 쪽이다. 따라서 배관이 더 먼저 부러진다. 만약 H-Beam의 굽힘 방향이 위 그림에 대하여 90° 회전한
방향이면 그 단면 2차 모멘트의 값이 절반 이하로 작아짐으로 Beam이 더 먼저 부러진다. 이와 같이
형상에 따라 값이 달라지는 단면 2차 모멘트는 굽힘에 저항하는 크기의 속성을 갖는다.
|
3. 위에서 사용한 Flex L 공식에 대한 재료 역학적 근거
|
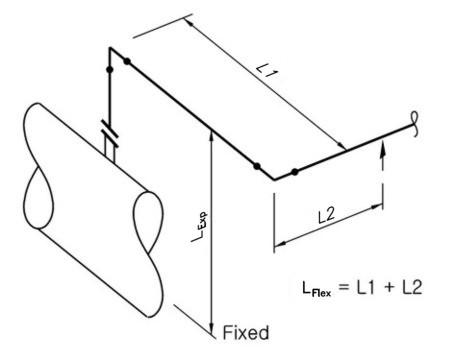
아래 그림과 같은 배관 Routing에서 열팽창에 의한 Thermal Stress는 일반적으로 굽힘이 많이 작용하는 Elbow 또는 Support
부위에서 크게 주어진다. 이 Stress 값이 적어도 Allowable 값 이하가 되는 임의의 Pipe Size에 대한 Minimum Flexible
Length를 구해보자. 배관의 온도는 200°C이고 재질은 Carbon Steel로 가정한다.
따라서 온도 200°C에서 열팽창계수 α = 12.24*10-6 mm/mm/C,
탄성계수 E = 1.951 * 106 kg/cm2,
Sa = 1406 kg/cm2를 적용한다.
ASME B31.3 Code에 의하면 Thermal 허용응력(Allowable Stress) 값(Sa)은
Sa = f * (1.25*Sc + 0.25*Sh), 또는 Sa = f * [1.25*(Sc+Sh) - SL]
(f: 피로계수, 보통 1임) 의 수식으로 주어지는데, Wgt/압력에 대한 허용응력을 모두 사용한
경우로 가정하고 Thermal 허용응력(Sa)을 Code에 의한 허용응력의 2/3(1406kg/cm2)로
가정하였다.
|
|
주어진 배관 Routing을 외팔보로 가정하여 처짐량이 배관의 열팽창 량과 같고, 이 때의 Bending Stress(Sb)가
Allowable Stress와 같다고 보면 열팽창량이 흡수되어지는 (어떠한 구속도 없는) Flexible Length는
다음과 같이 계산된다.

이것을 간단히 정리하면 구하고저 한 유연성이 요구되는 길이(Flexible Length)는
|
LFlex = 0.0254 * (T*LExp*OD)1/2 =>
LFlex = 0.0254 * (T*L*S)1/2
|
로 된다.
여기에서 온도 T의 단위는 °C이고, 열팽창을 하는 길이 L의 단위는 m이고,
배관 Size S의 단위는 Inch이다.
배관(뿐만이 아니라 철골 등)은 굽힘을 많이 받으면 스트레스를 많이 받는다. 팽창량이 흡수된다는 의미는 배관이
서서히 구부러져 그 Bending Stress가 적어도 Allowable 값 이하로 됨을 의미한다. 여기에서
이 LFlex은 열팽창을 하는 길이 LExp에 의하여 발생하는
팽창량을 흡수하는 Minimum Length를 의미한다. 따라서 보다 짧으면 굽힘을 더 많이 받음으로 Allowable값 이상의
Stress를 받게 된다. 이 Flex L 공식의 계수 0.0254은 200°C의 열패창율 값에서
25.4/1000으로 우연히 맞아 떨어진 값이다. 그러나, 300°C 정도의 배관에 적용해도 크게 문제되지는
않는다. 온도가 더 높으면 Allowable 값이 작아지고 또 열팽창율 값도 커짐으로, LFlex의
값을 계산된 값보다 더 크게 봐야 한다.
|
4. 배관의 Trim Elbow Angle 계산 공식 소개
임의의 방향으로 꺾어진 배관의 Trim Elbow Angle을 기하학적으로 계산하는 것은 몹시 어려우나, 배관 Routing을
Vector로 보고 벡터 Dot Product의 공식을 적용하면 매우 쉽다.
4.1 Vector
크기와 방향을 모두 갖는 물리량을 Vector라 한다. 대표적인 예는 힘, 속도, 운동량 등이다. Vector는 두 점을 있는
화살표로 표시할 수 있다. 화살의 길이는 Vector의 크기를, 화살의 방향은 Vector의 방향을 나타낸다.
|
|
4.2 Vector의 가법
두 벡터의 가법은 다음 그림에 보인 바와 같이 하나의 벡터 A의 종점에 벡터 B의 시점을 옮기고 벡터 A의 시점에서
벡터 B의 종점을 연결하는 것으로 정의된다.
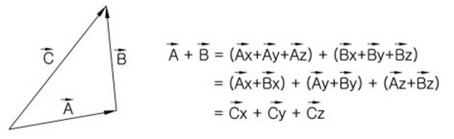
|
|
4.3 Vector Dot Product
다음 그림에서 물체에 힘 F를 가하여 스프링이 길이 L 만큼 압축되었을 때 스프링에 저장된 에너지는 두 벡터의
스칼라 적(곱)으로 표현된다. 이를 Vector Dot Product라고 한다. 이렇게 말하면 추상적으로 잘 이해가 되지
않을 수도 있음으로, 이렇게 바꾸어 생각하자. 힘을 가해서 스프링을 압축하면 에너지가 저장되는데, 가해지는
힘이 스프링을 압축하는 방향과 같으면 이 힘은 100% 활용되고, 가하는 힘이 스프링의 압축 방향과 수직으로
작용하면 이 힘은 아무런 작용도 하지 못하는 무용한 힘으로 버려짐을 가상하자. 이러한 관계를 수학적으로
표현한 것이 Vector Dot Product이다.
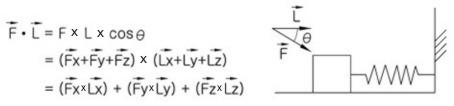
이 식을 활용하면 배관 Design에서 Elbow의 Trim Angle을 쉽게 계산할 수 있다. 위의 식에서 Dot(·)의
의미는 대수학에서 곱셈의 부호(x)와는 의미가 다른 Vector의 곱을 정의하는 기호이다. 아래 예제에서 구체적으로
확인할 수 있다.
Vector의 곱에는, 엄밀히 말해서, 위에 설명한 Dot Product 이외에 배관 디자인과는 직접적으로 관련이 없는
Cross Product가 있다. 수식으로는 A x B = A x B x sin(θ)로 표현하는데, 이는 사람이 크랭크를
돌리는 경우를 상상하면 이해가 빠르다. 크랭크 Lever에 수직한 방향으로 힘을 가하면 힘이 100%활용되어 크랭크를
회전시키는 토크로 변환되지만, 지레대에 나란한 방향으로 힘을 가할 경우에는, 이 힘은 크랭크를 회전시키는 데 아무런
작용도 하지 않는다. 이러한 관계를 수학적으로 표현한 것이 Vector Cross Product이다.
|
|
예제: 배관 Trim Angle 계산
아래 그림과 같은 배관 Routing에서 배관 Elbow의 Trim Angle을 구하라.
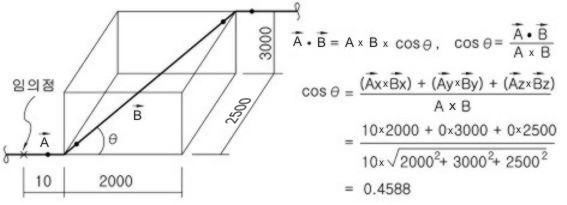
위에서 A⋅B는 Vector A와 B의 각 성분끼리의 곱이고, AxB은 Vector A와 B의 절대값의 곱,
즉, 배관 길이의 곱이다.
풀이:
위 그림에 보인 바와 같이, Line을 Vector A와 B로 보고 임의점을 잡아 Vector Product의
공식을 적용하면 쉽게 계산할 수 있다. 위 계산식에서 cos(θ)는 0.4588임으로 구하고자 하는
Angle은 θ = cos-1(0.4588) = 62.88°이다.
참고:
이와 같이 배관의 Trim Angle을 계산하는 S/W를 우측에 보인 "배관 응력해석 관련" "5. Util.Progs Download"에
올려두었으니 다운로드하여 사용하시기 바랍니다.
|




